Chapter 4: Machine Learning Pipeline¶
Now that we have a good understanding of how to gather different types of network data through measurement, we can begin to think about how to transform this data for input to machine learning models. While we often think about the process of machine learning as the modeling process, in fact the process of machine learning constitutes a larger pipeline that involves a sequence of the following steps:
Data Engineering
Model Training
Model Evaluation
We often refer to this process as the machine learning pipeline; the last chapter, we discussed the mechanics of the first part of this pipeline, data acquisition, in the context of network data—that is, different types of network measurement. In this chapter, we will discuss the pipeline as a whole. Generally, the machine learning pipeline applies to models that learn from labeled examples (supervised learning) as well as from data that does not have corresponding labels (unsupervised learning). We will focus initially in this chapter on how the pipeline applies to supervised learning, before turning to how it can be applied in the unsupervised context.
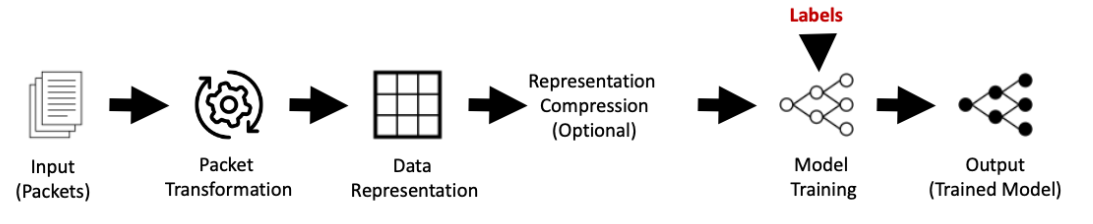
Figure 3. Machine learning pipeline.¶
Figure 3 illustrates the machine learning pipeline. Data engineering consists of taking data input and generating a representation appropriate for model training, associating labels with the examples in the data, and splitting the data into training and validation sets. Model training consists of learning a model from the training data. Model evaluation consists of evaluating the model on the validation data and, if necessary, tuning the model to improve its performance. The output of the pipeline is a model that can be used to predict labels for new examples.
Data Engineering¶
The first step in training any machine learning model is gathering the data and preparing it for input to a model. In the context of network data, the last chapter taught us how to gather different types of network data using different types of network measurement, as well as how to transform this data into features that may be relevant for training machine learning models, such as flows. In this chapter, we will take that process a step further, applying those techniques to create a labeled dataset for model input.
In the context of machine learning, a dataset is a collection of examples that are used to train a model. Each example is a collection of features that are used to predict a label. For example, in the context of network data, a dataset might consist of a collection of flows, where each flow is represented by a collection of features, and the label is the type of application that generated the flow.
The process of preparing a dataset for input to a model (i.e., for training) is sometimes called data engineering. This process consists of a number of steps, including cleaning the data, associating labels with the examples, and splitting the data into training, test, and validation sets. In this section, we will discuss each of these steps.
Cleaning Data¶
Machine learning models are only as good as the data that we provide them with for training. If the data itself contains errors, including incorrect or missing values, the resulting trained models will reflect those errors. Understanding the quality of data gathered from network measurements, such as those discussed in the last chapter, is an important part of the data cleaning process and is a relatively well-understood practice within the context of Internet measurement. Vern Paxson’s “Strategies for Sound Internet Measurement” provides a more extensive introduction to the topic of understanding and cleaning data gathered from network measurements. Here, we offer a few brief pointers on cleaning network data, inspired by some of the insights from Paxson’s paper, with additional insights as they pertain to machine learning.
Understanding the Data¶
An important step towards using data for machine learning is understanding the nature and characteristics of the data. This step is important for a number of reasons. First, it helps us understand the quality of the data, including critical aspects such as the size of the dataset, where the data was gathered, and so forth. Second, a deeper exploration can help us understand the characteristics of the data that may ultimately lead us to defining features that improve classification accuracy.
Before exploring any dataset in detail, it is helpful to understand basic characteristics concerning its size, and the nature of the data. Let’s continue with the simple example from last chapter, where we loaded a packet trace into a Pandas dataframe and generated features.
Before we proceed with feature generation or machine learning, however, we
should understand some basics from out dataset, including, for example, how
many packets are in the dataset, the start and end times of the dataset,
minimum and maximum packet lengths and so forth. We can use the describe
method of the Pandas dataframe to get a summary of the dataset. The example
below shows an example of the output of the describe method for the
dataframe from the last chapter to enable some sanity checking of
the data.
The output from this exercise is a helpful sanity check. The “shape” command
shows us how many rows and columns that we have in our data (specifically, the
number of rows, corresponding to the number of packets; and the number of
columns, corresponding to the number of features). The describe command
shows us some basic statistics about the data, including the minimum and
maximum values for each feature, as well as the mean and standard deviation
for each feature. The head command shows us the first few rows of the
dataset; the tail command shows us the last few rows of the dataset; and the
info command shows us the data types of each column, all of which can be
helpful for sanity checking the data.
For example, we can see the minimum and maximum values for the length of each packet: 60 bytes and 1514 bytes, respectively. These values should make sense, given our domain knowledge about network traffic and packet maximum transmission unit (MTU). Similarly, we see that the minimum port number is 53 (a well-known service port for DNS), and the maximum port is less than 65536 (the maximum allowable port number, given that the field is only 16 bites).
Extracting features from a packet capture with netml.
from netml.pparser.parser import PCAP
pcap = PCAP('../examples/notebooks/data/http.pcap')
pcap.pcap2pandas()
pdf = pcap.df
pdf = pdf[['datetime', 'ip_src', 'port_src', 'ip_dst', 'port_dst', 'length']]
# Example sanity checking of data.
print("\n\nDimension of data: {}".format(pdf.shape))
# Print minimum and maximum times.
print("\n\nMin time: {}\nMax time: {}".format(min(pdf['datetime']), max(pdf['datetime'])))
# Describe the dataframe.
pdf.describe()
WARNING: No IPv4 address found on anpi0 !
WARNING: No IPv4 address found on anpi1 !
WARNING: more No IPv4 address found on en3 !
Dimension of data: (24798, 6)
Min time: 2022-09-29 20:24:42
Max time: 2022-09-29 20:25:30
| port_src | port_dst | length | |
|---|---|---|---|
| count | 24798.000000 | 24798.000000 | 24798.000000 |
| mean | 9572.610452 | 51357.588475 | 1176.372611 |
| std | 21482.363472 | 21937.801421 | 580.866842 |
| min | 53.000000 | 53.000000 | 60.000000 |
| 25% | 443.000000 | 60895.000000 | 1292.000000 |
| 50% | 443.000000 | 60964.000000 | 1494.000000 |
| 75% | 443.000000 | 60988.000000 | 1510.000000 |
| max | 65429.000000 | 65429.000000 | 1514.000000 |
Understanding the distribution of features can also help us understand which features may be useful for a particular classification problem. For example, in the example above, we might hypothesize that there is a relationship between the length of a packet and the type of application that generated the packet, or the direction of traffic. We can test this hypothesis by plotting the distribution of packet lengths for each port number, as shown below.
Dealing with Outliers¶
Inevitably, data gathered from real-world network measurements will often contain outliers. Outliers exist in many datasets, and there are many possible ways to deal with them. The first step in dealing with outliers is to identify them. One way to identify outliers is to use a box plot, which is a common way to visualize the distribution of data. A box plot is a graphical representation of the distribution of data, where the box represents the interquartile range of the data, and the whiskers represent the minimum and maximum values of the data. Outliers are typically represented as points outside of the whiskers. The example below shows a box plot of the minimum and maximum packet lengths for each flow in the dataset we explored with netml from the last chapter.
Exploring the distribution of packet lengths to identify outliers.
import matplotlib.pyplot as plt
# create a boxplot using matplotlib
fig, ax = plt.subplots()
# Explore the distribution of `netml` features
ax.boxplot([features[8], features[9]])
ax.set_xticklabels(['Minimum Lengths', 'Maximum Lengths'])
# set labels for the plot
ax.set_title('Packet Lengths for Each Flow')
ax.set_yscale('log')
ax.set_ylabel('Column Name')
# show the plot
plt.savefig('pipeline_length-boxplot.png')
plt.show()

Labeling Data¶
Supervised machine learning requires training models on labeled data. In this section we’ll talk about why data needs labels, as well as the process of labelling data for different types of prediction problems.
Why Data Needs Labels¶
The goal of supervised machine learning is to use labeled data to train a model that can the predict correct labels (sometimes referred to as targets or target predictions) for data points that the model did not see when it was being trained.
As a human analogue, supervised machine learning is akin learning how to solve a general problem by seeing the “correct” answer to several specific instances and identifying more general patterns that are useful for solving any instance of the task. For example, when driving, you know that the correct action when seeing a stop light is to bring your car to a halt, even though you may have never seen that specific stop light at that instance ever before. In the context of networking, then, many such examples exist. A machine learning model might automatically recognize an attack or traffic from a specific application based on “signature” properties, even though the model has never before seen that specific traffic trace.
Any use of supervised learning to solve a problem must thus necessarily involve the collection of labeled training data. Training data typically has two aspects: examples (i.e., multi-dimensional data points) and labels (i.e., the “correct answers”). The training examples are observations or data points. The training labels consist of the “correct” categories or values that a trained machine learning algorithm should assign to each of the training examples.
In addition to training examples, creating a supervised machine learning model also requires an associated label for each set of feature. For single-label learning tasks, there will be a single label for every example in the data set. So if you have a matrix of training examples with 20 rows, you will need to have 20 labels (one for each example). The training labels are thus typically represented as a vector with the same number of elements as the number of training examples. For instance, each training label for a security task might be a 1 if the corresponding example corresponds to malicious traffic, or a 0 if the corresponding example is benign.
For multi-label learning tasks, the data may be associated with multiple label vectors or a combined label matrix. For example, you might want to predict users’ responses to a quality of experience questionnaire. For each question on the questionnaire, you would need a label corresponding to each user. For convenience, the vector (or matrix, for multi-label tasks) of training labels are usually given the variable name y. The first dimension of the training labels is the same cardinality as the first dimension of the training examples.
The example below shows an example of labeling data, based on two loaded packet captures. The first trace is a packet capture of benign traffic, and the second is a trace of HTTP scans for the log4j vulnerability. The example shows the use of netml to load the packet captures and extract features and the subsequent process of adding a label to each of the resulting data frames, before concatenating the two frames and separating into X and y, for eventual input to training a machine learning model.
Labeling data for supervised machine learning.
hpcap = PCAP('../examples/notebooks/data/http.pcap', flow_ptks_thres=2, verbose=0)
lpcap = PCAP('../examples/notebooks/data/log4j.pcap', flow_ptks_thres=2, verbose=0)
# extract flows from pcap
hpcap.pcap2flows()
lpcap.pcap2flows()
# extract features from each flow via IAT
lpcap.flow2features('IAT', fft=False, header=False)
ld = pd.DataFrame(lpcap.features)
# extract features from each flow via IAT
hpcap.flow2features('IAT', fft=False, header=False)
hd = pd.DataFrame(hpcap.features)
hds = hd.loc[:,:4]
hds.shape
# label the normal and anomalous HTTP traffic traces
pd.set_option('mode.chained_assignment', None)
hds['label'] = 0
ld['label'] = 1
# concatenate the two data frames
data = pd.concat([ld,hds])
# separate into features and labels
X = data.loc[:,:4]
y = data['label']
Labeling for Prediction Problems¶
The format of the training labels distinguishes regression problems from classification problems. Regression problems involve labels that are continuous numbers. Classification problems involve discrete labels (e.g. integers or strings). Classification tasks can be further categorized into binary classification and multi-class classification by the number of distinct labels. While some supervised machine learning algorithms can be trained to perform either classification or regression tasks, others only work for one or the other. When choosing a machine learning algorithm, you should pay attention to whether you are attempting a classification or regression task. Our description of common machine learning models in the next chapter clearly states whether each algorithm is applicable to classification, regression, or both.
Regression. Training labels for regression problems are simply encoded as real-value numbers, usually as a floating point type. Regression may be familiar if you have experience fitting lines or curves to existing data in order to interpolate or extrapolate missing values using statistics techniques. Regression problems can also be performed with integer labels, but be aware that most off-the-shelf regression algorithms will return predictions as floating point types. If you want the predictions as integers, you will need to round or truncate them after the fact.
Binary Classification. Training labels for binary classification problems are encoded as 1s and 0s. The developer decides which class corresponds to 1 and which class corresponds to 0, making sure to keep this consistent throughout the ML training and deployment process.
Multi-class Classification: Training labels for multi-class classification problems are encoded as discrete values, with at least three different values represented in the vector of training labels y. Note that multi-class classification (more than two discrete classes) is distinct from multi-label classification (multiple independent classification tasks, each with their own set of discrete classes). There are multiple options for encoding training labels in multi-class classification problems. Since most machine learning algorithms require training labels as numeric types (e.g. int, float, double), string class names usually need to be encoded before they can be used for ML training (decision trees are a notable exception to this requirement). For example, if you have labels indicating users’ quality of experience on a “poor”, “acceptable”, “excellent” scale, you will need to convert each response into a number in order to train an algorithm to predict the QoE of new users.
One way to perform encoding for multi-class classification is to assign each class to a unique integer (ordinal encoding). In the example above, this mapping could convert “poor” –> 0, “acceptable” –> 1, and “excellent” –> 2. The fully encoded training labels would then be a vector of integers with one element for each training example. Another way to encode multi-class training labels is to perform one-hot encoding, which represents each class as a binary vector. If there are N possible classes, the one-hot encoding of the ith class will be an N-element binary vector with a 1 in element N and a 0 in all other elements. In the example above, this mapping could convert “poor” –> [1,0,0], “acceptable” –> [0,1,0], and “excellent” –> [0,0,1].
Although it is useful to understand these subcategories of supervised learning, it is also wise not to assign excessive importance to their distinctions. Many machine learning algorithms are effective for either classification or regression tasks with minimal modifications. Additionally, it is often possible to translate a classification task into a regression task, or vice versa. Consider the example of predicting improvements in last-mile network throughput for different possible infrastructure upgrades. While it is reasonable to express throughput as a real-valued number in Mbps, you may not care about small distinctions of a few bits per second. Instead, you could reframe the problem as a classification task and categorize potential updates into a few quality of experience classes.
Dividing Data¶
Once the data is labeled, we can use the data to train a machine learning model. Before we can do so, we need to divide the data into training and testing sets. The training set is used to train the model, and the testing set is used to evaluate the model’s performance. Additionally, in the process of training, a subset of the training data is often withheld from the model to perform validation (i.e., to evaluate the model’s performance during training), to help tune a model’s parameters. We explore each of these concepts with examples below.
Training and Testing Sets¶
The goal of supervised learning is to train a model that takes observations (examples) and predicts labels for these examples that are as close as possible to the actual labels. For instance, a model might take traffic summary statistics (e.g., IPFIX records) as input features and predict quality of experience labels (or target predictions), with the goal that the predicted labels are as “close” as possible to the actual quality experienced by the customer.
However, if you don’t know the correct labels for new observations, how do you measure whether the model is succeeding? This is an important question and one that must be considered at the beginning of the ML process. Imagine that you’ve trained a machine learning algorithm with training examples and training labels, then you deploy it in the wild. The algorithm starts seeing new data and producing predictions for that data. How can you evaluate whether it is working?
The way to solve this problem is to test the performance of the trained algorithm on additional data that it has never seen, but for which you already know the correct labels. This requires that you train the algorithm using only a portion of the entire labeled dataset (the training set) and withhold the rest of the labeled data (the test set) for testing how well the model generalizes to new information.
Splitting data into training and test sets.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
The examples that you reserve for the test set should be randomly selected to avoid bias in most cases. However, some types of data require more care when choosing test set examples. If you have data for which the order of the examples is particularly important, then you should select a random contiguous subset of that data as your test set. That maintains the internal structure that is relevant for understanding the test examples. This is particularly important for chronological data (e.g. packets from a network flow). If you do not select a contiguous subset, you may end up with a nonsensical test set with examples from one day followed by examples from a year later followed by examples from a few months after that.
This brings us to the golden rule of supervised machine learning: never train on the test set! Nothing in the final model or data pre-processing pipeline should be influenced by the examples in the test set. This includes model parameters and hyperparameters (more below). The test set is only for testing and reporting your final performance. This allows the performance evaluation from the test set to be as close of an approximation as possible to the generalization error of the model, or how well the model would perform on new data that is independent but identically distributed (i.i.d.) to the test set. For example, when you report that your model performed with 95% accuracy on a test set, this means that you also expect 95% accuracy on new i.i.d. data in the wild. This caveat about i.i.d. matters, because if your training data and/or test set is not representative of the real-world data seen by the model, the model is unlikely to perform as well on the real-world data (imagine a trained Chess player suddenly being asked to play in a Go tournament).
The best way to avoid breaking the golden rule is to program your training pipeline to ensure that once you separate the test set from the training set, the test set is never used until the final test of the final version of the model. This seems straightforward, but there are many ways to break this rule.
A common mistake involves performing a pre-processing transformation that is based on all labeled data you’ve collected, including the test set. A common culprit is standardization, which involves normalizing each feature (column) of your dataset such that variance matches a prespecified distribution with mean of zero. This is a very common pre-processing step, but if you compute standardization factors based on the combined training and test set, your test set accuracy will not be a true measure of the generalization error. The correct approach is to compute standardization factors based only on the training set and then use these factors to standardize the test set.
Another common mistake involves modifying some hyperparameter of the model after computing the test error. Imagine you train your algorithm on the training set, you test it on the test set, and then you think, “Wow, my test accuracy was terrible. Let me go back and tweak some of these parameters and see if I can improve it.” That’s an admirable goal, but poor machine learning practice, because then you have tuned your model to your particular test set, and its performance on the test set is no longer a good estimate of its error on new data.
Validation Sets¶
The correct way to test generalization error and continue to iterate, while still being able to test the final generalization error of the completed model, involves dividing your labeled data into three parts:
a training set, which you use to train the algorithm,
a test set, which is used to test the generalization error of the final model, and
a validation set, which is used to test the generalization error of intermediate versions of the model as you tune the hyperparameters.
This way you can check the generalization performance of the model while still reserving some completely new data for reporting the final performance on the test set.
If the final model performs well across the training, validation, and test sets, you can be quite confident that it will perform well on other new data as well. Alternatively, your final model might perform well on the training and validation sets but poorly on the test set. That would indicate that the model is overly tuned to the specificities of the training and validation sets, causing it to generalize poorly to new data. This phenomenon is called overfitting and is a pervasive problem for supervised machine learning. Overfitting has inspired many techniques to avoid and mitigate, several of which we describe below.
While dividing your labeled data into training, validation, and test sets works well conceptually, it has a practical drawback. The amount of data used to actually train the model (the training set) is significantly reduced. If you apply a 60% training, 20% validation, 20% test split, that leaves only 60% of your data for actual training. This can reduce performance, because supervised ML models generally perform better with more training data.
The solution to this is to use a process called cross validation, which allows you to combine the training and validation sets through a series of sequential model trainings called folds. In each fold, you pull out a subset of the training data for validation and train the model on the rest. You repeat this process with non-overlapping subsets for each fold, such that every training example has been in a validation fold once. In a 5-fold cross-validation, each fold would use 20% of the non-test data as a validation set and the remaining 80% for training. This would result in 5 different validation performance measurements (one for each folds) that you can average together for the average cross-validation performance.
Cross-validation provides a more robust measure of generalization performance than fixed training and validation sets. It is so common that supervised machine learning results are often reported in terms of the average performance on an N-fold cross-validation.
So how many folds is enough? Generally, the more folds, the better estimation of model performance. In the extreme case, called leave-one-out cross-validation, each fold uses a validation set with just one example, allowing the rest to be used for training. Each fold tests whether the model correctly predicts this one example when trained on all other examples. This provides the best estimate of generalization performance, because you’re training with the most data possible. If you have labeled 100 examples in your non-test set, leave-one-out cross-validation involves performing 100 folds and averaging the accuracy across across all 100. You can then repeat this process while tuning model hyperparameters to check the effects on generalization accuracy.
Unfortunately, leave-one-out cross-validation has its own drawbacks. Every cross-validation fold involves training a model, and if the training process is resource intensive, leave-one-out cross-validation can take a long time. Some models, especially neural network models, take a long time to train, so doing more than a few folds becomes impractical. For such models, a smaller number of folds (often 5 or 10) are used in practice.
Model Training¶
Training a supervised machine learning model involves adjusting the model’s parameters to improve its ability to predict the training labels from the training examples. This adjustment process takes place automatically, typically using an iterative algorithm (such as gradient descent) to gradually optimize the model’s parameters. If the training process works correctly, it will produce a model that performs as well as possible on the training set. Whether or not this trained model will generalize to new data must be tested using a validation and/or test set.
Model training.
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(random_state=0,
n_jobs=-1,
n_estimators=100,
class_weight='balanced')
# Train the model using the training sets y_pred=clf.predict(X_test)
rf.fit(X_train,y_train)
# prediction on test set
y_pred = rf.predict(X_test)
It is important to note the difference between model parameters and hyperparameters.
Parameters are the elements of the model that the training algorithm automatically modifies when attempting to improve the model’s performance on the training set.
Hyperparameters* are “meta”-parameters that can be tuned manually or automatically, depending on the degree to which the model creation process is automated.
Model training is a minimization process. Each training step attempts to modify the model’s parameters to reduce the difference, or error, between the labels predicted by the model and the actual training labels. You can choose which error function you want the training process to minimize. Square error, square difference, or absolute error are good for regression problems, while others, such as categorical cross-entropy, are better for classification problems. We’ll define and see equations for once we start looking at training of specific model types.
How Training Works: Error Minimization¶
A few combinations of models and error functions have closed form solutions for minimization, allowing you to directly solve for the optimal model parameters. However, most models and error function combinations used in practice either don’t have a closed form solution or the computation cost of the closed form solution is infeasible. The solution is to apply an iterative process, usually a version of gradient descent, starting with arbitrarily chosen initial parameter values and incrementally improving them until values close to the optimal are found.
Gradient descent is a mathematical representation of the idea that if you can’t see the solution to a problem, just repeatedly take one step in the right direction. By computing or approximating the gradient of the error of a model with respect to the model’s parameters, it is possible to update the parameters “down” the gradient and improve the model’s performance. Computing or approximating a gradient is often easier than directly solving for a minimum, making gradient descent a feasible way to train many types of complex models.
The size of “step” that each parameter takes during each gradient descent iteration can be turned using a hyperparameter called the learning rate. A high learning rate will update the parameters a relatively large amount with every step, while a low learning rate will update your parameters a small amount with every step. There exist many algorithms for dynamically tuning the learning rate during the training process to improve training speed while avoiding some common pitfalls of gradient descent (more on these below). In practice, you will likely use one of these existing algorithms rather than controlling the learning rate manually.
The gradient descent process continues until the model parameter stop changing between iteration (or at least until they change less than a predetermined small value). When this happens, the parameters define a model that is in a local minimum of the error function, which is hopefully close to the optimum.
There are a few variations to gradient descent that gain even more computational efficiency. The first, batch gradient descent uses the entire training data set to compute the gradient at each iteration. This provides an accurate gradient value, but may be computationally expensive. An alternative approach, stochastic gradient descent uses only a single example from the training set to estimate the gradient at each iteration. After N iterations, all N examples in the training set will have used for a gradient estimate once. Stochastic gradient descent allows for faster parameter update iterations than batch gradient descent, but the estimated gradients will be less accurate. Whether or not this results in a faster overall training time depends on the specifics of the model and the training set. Mini-batch gradient descent is a third option that allows for a tradeoff between the extremes of batch and stochastic gradient descent. In mini-batch gradient descent, a hyperparameter called the batch size determines how many training examples are used to estimate the gradient during each iteration.
This provides a great deal of flexibility, but introduces the need for one more term frequently used when discussing model training: the epoch. One epoch is one sequence of gradient descent iterations for which each example in the training set is used to estimate exactly one gradient. In batch gradient descent, iterations are equivalent to epochs, because all training data is used for the gradient calculation. In stochastic gradient descent, each epoch consists of N iterations for a training set with N examples. The number of iterations per epoch in mini-batch gradient descent depends on the batch size. With N training examples and a batch size of B, there will be ceiling(N/B) iterations per epoch.
Gradient descent is the heart of machine learning, but it’s not without problems. Many ML models, especially deep learning models, have gradients that are non-convex, so rather than converging on the global minimum, gradient descent gets stuck in a local minimum or plateau and is unable to make further progress. Getting stuck in a plateau is known as the vanishing gradient problem and especially plagues deep learning models. Fortunately, algorithms that dynamically modify the learning rate during training can help avoid these situations. For example, the simulated annealing algorithm starts with a large learning rate and graduate decreases the rate throughout the learning process, making it less likely that the process gets stuck far away from the global minimum.
Bias-Variance and Overfitting¶
Overfitting is a common problem for many supervised machine learning models. An “overfit” model has been overly tuned to idiosyncracies of the training set and doesn’t generalize well to new data.
Machine learning models can either be underfit or overfit. An underfit model is too restrictive and fails to capture the relevant structure or details of the data being modeled. For example, fitting a linear function to a dataset with nonlinear characteristics would result in an underfit model. On the other hand, an overfit model is too permissive and captures noise or random fluctuations in the data, which may not generalize well to new, unseen data.
The balance between bias and variance is crucial in machine learning. If a model is too biased or has high bias, it may oversimplify the data and result in poor performance on both the training and test data. On the other hand, if a model has high variance, it may overfit the training data and perform poorly on the test data.
It’s useful to be able to detect when your model is overfitting. One way is to compare the model’s training error and validation error when trained on increasing fractions of the training set or for increasing number of gradient descent steps. As long as the training error is close to the validation error, you can be fairly confident that the model isn’t overfitting (and is likely underfitting, requiring more training data or training iterations to improve its performance). If the validation error is significantly worse than the training error, the model is likely overfitting.
To balance the trade-off between bias and variance, we need to tune our machine learning models. One common approach is regularization, which involves adding penalties or constraints to the model to prevent it from becoming too complex. Regularization techniques such as L1 and L2 regularization can help reduce the variance of a model by constraining the weights of the model during training.
There are several ways to deal with overfitting. The best approach is to collect more training data such that your training set is more representative of any new data the model will see in the wild. Another approach, early stopping involves stopping the training process when the training error and validation error start to diverge. Regularization places a penalty on parameter complexity during the training process, helping to prevent the model from becoming overly tuned to the training examples.
Another approach is to use ensemble methods, such as bagging and boosting, which combine multiple models to reduce variance and improve overall performance. Bagging involves training multiple instances of the same model on different subsets of the training data, while boosting involves combining the predictions of multiple weak models to create a stronger model.
Additionally, cross-validation can be used to assess the performance of a model and select the best hyperparameters or model configurations
Model Evaluation¶
Before we dive into learning about machine learning algorithms, we need to define a few more concepts to help us determine whether these algorithms are meeting their goals. First, we need to define what we mean by “close to the real label.” This is another way of saying “how do we measure the success (or accuracy) of the model?”
There are many performance metrics that we can use to evaluate a machine learning model. In general, these metrics compare predictions that a trained model produces to the correct labels and produce a value or other indication (e.g., a curve) that reflects the performance of the model.
Performance Metrics¶
For regression problems, you’ll often use an error function like mean squared error or mean absolute error. In this example, we have some data points, we’ve plotted a linear regression line, we could see the errors of the points off of the line. And you could report the average of those errors are the average of those squared errors as the performance of your model. The training process will attempt to minimize this error to produce a regression model that produces predictions which are as close as possible to all data points on average.
For classification, we can’t use mean or absolute errors directly, because the class labels are not real-valued and may not be ordinal.
Accuracy. is popular performance metric for classification problem because it is intuitive. The accuracy of a model is the ratio of correct predictions to all predictions. For some problems, this works pretty well. But for others just reporting accuracy is deceptive.
Imagine you’re training a machine learning algorithm to take in packets and classify them as “malicious” or “benign”. If you just use the naive algorithm “always predict benign”, the accuracy will be high accuracy, because most most packets aren’t malicious. So if you have a problem for which the actual classes aren’t evenly balanced among all of the possible classes, your accuracy score isn’t going to be as intuitive as it should be. For example, you shouldn’t necessarily assume that anything over 50% accuracy is great. 50% only a meaningful metric if you are doing binary classification where you’re expecting even numbers of both classes examples. In multi-class problems or tasks where certain classes are rare, accuracy isn’t a great way to report your results.
Accuracy
from sklearn.metrics import accuracy_score
# Compute accuracy
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: {}".format(accuracy))
Accuracy: 0.9891944990176817
Precision and Recall. Another way to report classification performance accuracy for multi-class and non-balanced classes is with a precision or recall score. These scores are best understood in the context of binary classification tasks. The precision score is the percentage of the elements that you correctly predicted were in a class of interest. A high precision score is good. You want most of the things that you predicted to be in that particular class to actually be in that class. The recall score is the number of things actually in a class of interest that you predicted were in that class. Prediction and recall are often two sides of a coin. You will see that if you make parameter or hyperparameter changes to improve precision, you may end up reducing recall (and vice versa). (ADD TRUE POSITIVES ETC.)
A high precision algorithm may not make many predictions, but when it does, it’s right. A high recall algorithm may make a lot of predictions hitting most of the examples in the class of interest, but also a bunch of examples ones that we didn’t care about. In different real world situations, you might want to tune your algorithm to have a higher precision or a higher recall, depending on your application.
For example, consider a machine learning system that is detecting malware in a mission critical system. It may not matter if there are some false alarms (low precision), but you want to make sure the system doesn’t miss any actual malware events (high recall). In comparison, consider spam detection. You may be okay with your spam detector allowing some spam through to the inbox (low recall), but you don’t want the detector to accidentally classify any non-spam messages as spam (high precision).
Since you can tune many algorithms to trade off precision and recall, you’ll often plot a precision/recall curve that shows how the tuning of some parameter affects precision and the recall. An ideal algorithm will have a curve that is one where precision remains high (close to 1) for all recall values.
Now, if you aren’t sure where to pick on this curve, you’ll often choose the like the Pareto optimal setting where any trade off that you make in one direction is outweighed by the trade off that you’d make in another direction. And if you’re familiar with Pareto optimality from economics, it’s exactly the same idea.
F1 Score. Sometimes you want to report a single number that says how well your algorithm performs instead of both precision and recall scores. The standard approach is to report an F1 score, which is the harmonic mean of precision and recall. The harmonic mean causes the F1 score to weigh low values higher. This means that a high precision won’t offset a particularly low recall or vice versa.
F1 Score
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_pred)
print("F1 Score: {}".format(f1))
F1 Score: 0.9942257217847769
Receiver Operating Characteristic. The receiver operating characteristic (ROC) is another performance measure that uses the true positive rate and the false positive rate. The true positive rate is exactly the same as recall, it’s just another name for the same concept. The false positive rate is a little different from precision. The false positive rate is the fraction of examples that we labeled as the class of interest but we were incorrect about. TPR and FPR are often used in terms of epidemiology.
Just like for precision recall, you can tune hyper parameters to affect the true positive rate and false positive rate. You can plot them on a curve called an ROC curve. As you change the parameter to increase the true positive rate, you may end up with more false positives, too. If you want a single metric to use for the algorithm performance that incorporates the fact that you can tune these parameters, you can use the area under the ROC curve. Since your algorithm would ideally be able to achieve a high true positive rate with a very low false positive rate, you’d have a curve that is right along the edge of the graph. The ideal area under the curve (AUC) is 1.
Confusion Matrices. Confusion matrices go beyond a single number or a scalar metric for classification performance and instead provide details about how your model is making mistakes. A confusion matrix plots the frequency or the number of examples that were given a particular label versus the correct label. If your model is doing perfectly, you will end up with a diagonal matrix where all of the examples are in the correct class. If your model is sometimes making mistakes, there will be numbers outside of this diagonal. You can then investigate these examples to see why they might be more difficult for the model and focus on these cases to improve your performance. Confusion matrices are useful for debugging and iterative improvements. The
Confusion matrix for evaluating the results of a classifier on test data.
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
print(metrics.confusion_matrix(y_test, y_pred))
cm = confusion_matrix(y_test, y_pred, labels=rf.classes_)
disp = ConfusionMatrixDisplay(confusion_matrix=cm,
display_labels=rf.classes_)
disp.plot()
# show the plot
plt.savefig('pipeline_confusion-matrix.png')
plt.show()
[[ 60 8]
[ 3 947]]


